Overfitting and Underfitting in terms of Model Validation

In the previous post, we’ve learned K-fold cross validation method for splitting the whole dataset in terms of model selection.

If you are not sure about this topic,
check here: K-fold Cross Validation for model selection in ML

In this post, we will learn:

1. Two most common problems of models by model validation: Overfitting and Underfitting
2. What a good model actually is.

When validating a model, we check how well the model will predict for an unseen data in the future.

A poor model can show either overfitting or underfitting when validating the model performance during training.

The model with overfitting or underfitting has no power of generalization, which means that it cannot predict well for an unseen data.

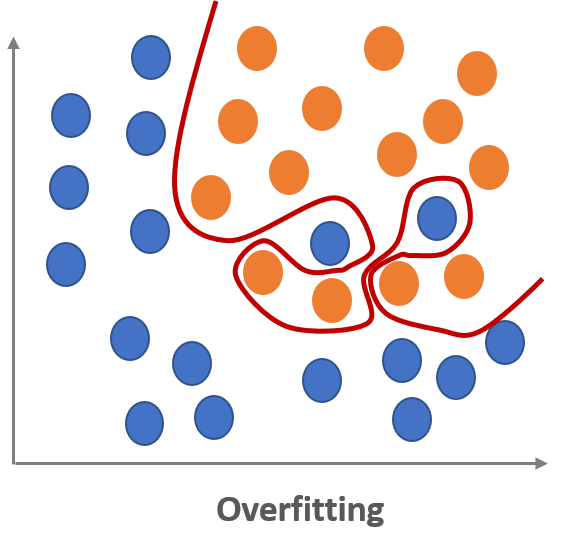
Overfitting means that the model is too fit to the training dataset.
The overfitted model cannot work well on a new dataset since it is tailored to the specific training dataset.
It is like the model did not learn the patterns of the training data set, but just memorized all the details of the training dataset including its noises.

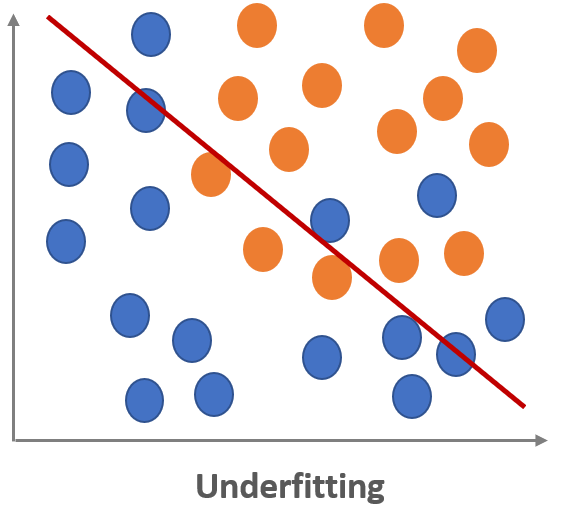
Underfitting means that the model is even not fit to the training dataset.
The underfitted model cannot work well on a new dataset since it is not even work well on the training dataset.
One possible cause is that the model could not learn enough because of insufficient training dataset.

What we need to do is find a good model that shows an optimal fitting between underfitting and overfitting.

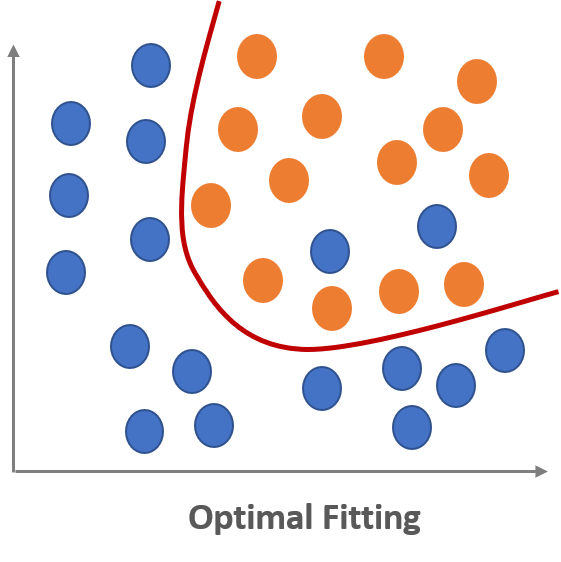
For the optimal fitting of a good model, we need to know the concept of the bias-variance trade-off.

Here is the quick overview regarding the concept.

• Overfitting: A model with low bias and high variance
• Underfitting: A model with high bias and low variance
• Optimal Fitting: A model with low bias and low variance

In the next post, we will learn:

1. What is Bias and Variance
2. What is Bias-Variance Trade-Off

References

• Reference1: Overfitting and Methods of Addressing it
• Reference2: Model Validation: Problem Areas and Solutions – Overfitting and Underfitting
• Reference3: What is Overfitting in Computer Vision? How to Detect and Avoid it
• Reference4: What is underfitting and overfitting in machine learning and how to deal with it.
• Reference5: Overfitting and Underfitting With Machine Learning Algorithms
• Reference6: Overfitting and underfitting in machine learning
• Reference7: Epoch vs Batch Size vs Iterations

---