Evaluation of a model for classification problem (Part 1)

How do we evaluate the quality of a trained model? In classification problems, we can check how often a class is predicted correctly by the model. In the part 1, we first deal with the binary classification problem, which will be the base for the multiclass classification problem in the part 2.

At the end of the article, we can answer to the questions:

1. What are "TP", "FP", "FN" and "TN" in a "Confusion Matrix"?
2. What are "Accuracy" (Bonus: "Accuracy Pardox"), "Precision", "Recall" and "F1-Score"?

Binary Classification

The goal of a model for a binary classification problem is to classify two classes well.

For example, we can imagine that our model is a rapid testkit for corona virus, which are designed to detect a person who has corona virus.
Then, two classes for the model are:

• CLASS 1: “has Corona” (positive)
• CLASS 2: “has no Corona” (negative)

For the two classes, there are four cases resulting by the testkit.

• CASE 1: The result of the testkit is positive AND the person has actually corona virus → "TP" (True Positive)
• CASE 2: The result of the testkit is positive BUT the person does not have corona virus → "FP" (False Positive)
• CASE 3: The result of the testkit is negative BUT the person has actually corona virus → "FN" (False Negative)
• CASE 4: The result of the testkit is negative AND the person does not have corona virus → "TN" (True Negative)

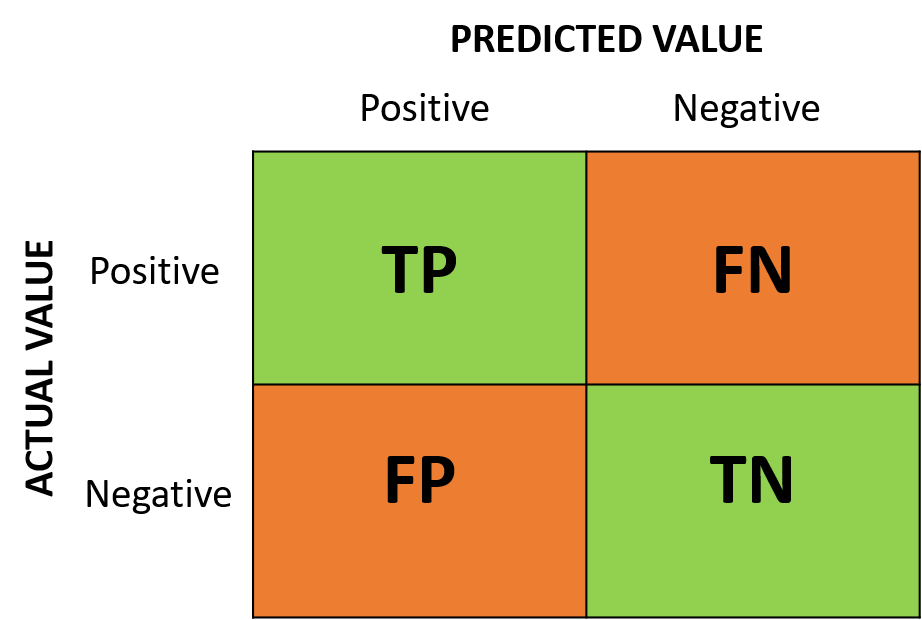
The images above are called "Confusion Matrix" and we can easily see the four cases mentioned above in the each cell of the confusion matrix.

For the purpose of the testkit, the case 1 and the case 4 are the right predictions by the model because it detected the person who has actually corona virus (TP) and the person who does not have corona virus (TN) correctly. The right predictions by the model are marked GREEN in the confusion matrix.

The case 2 and the case 3 are the wrong predictions by the model becaus it predicted wrong that the person who does not have corona virus as positive (FP) and who does have corona virus as negative (FN). The wrong predictions by the model are marked ORANGE in the confusion matrix.

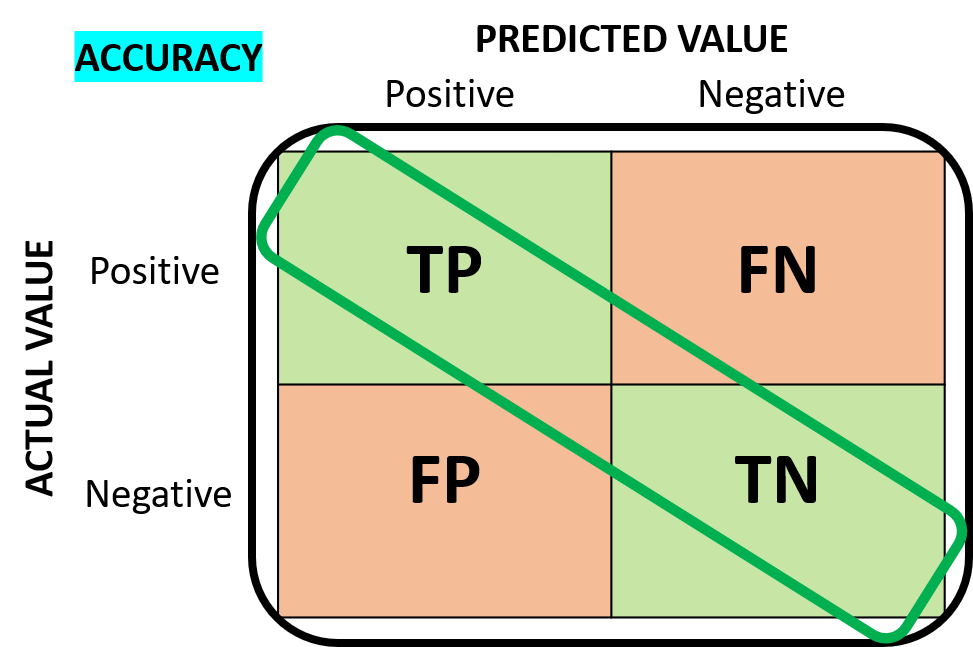
With the confusion matrix, we can simply visualize how to calculate the four metrics “Accuracy”, “Precision”, “Recall”, and “F1-Score” in order to evaluate the performance of the trained model.

The following confusion matrix shows the four cases with their number of instances by the model:

The total number of the predicted instances are 10,000, which is the sum of the four cells.

Total number of instances: TP(9040) + FP(151) + FN(68) + TN(741) = 10,000

Now we are going to learn what are exactly the four metrics and how we calculate them.

Accuracy

"Accuracy" tells us how many correct predictions are made from the total predictions.

Correct predictions for the corona testkit are TP(9040) and TN(741).
Total predictions by the testkit are TP(9040) + FP(151) + FN(68) + TN(741)

This is the formula how we calculate the accuracy:

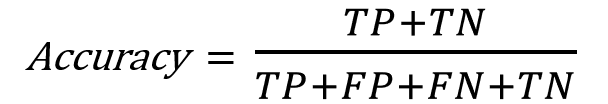
And this is the accuracy of our model:

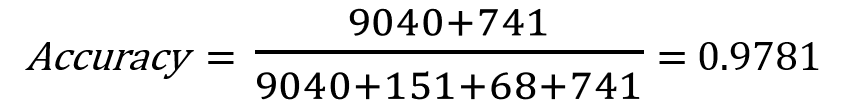
Accuracy seems like a quite simple and good metric to evaluate the performance of a model.
But there are tricky cases to evaluate a model only with Accuracy.

Accuracy Paradox

Let’s assume that our model is spam email filter.

We have two models for the spam filter.
What are the accuracy of the two models?

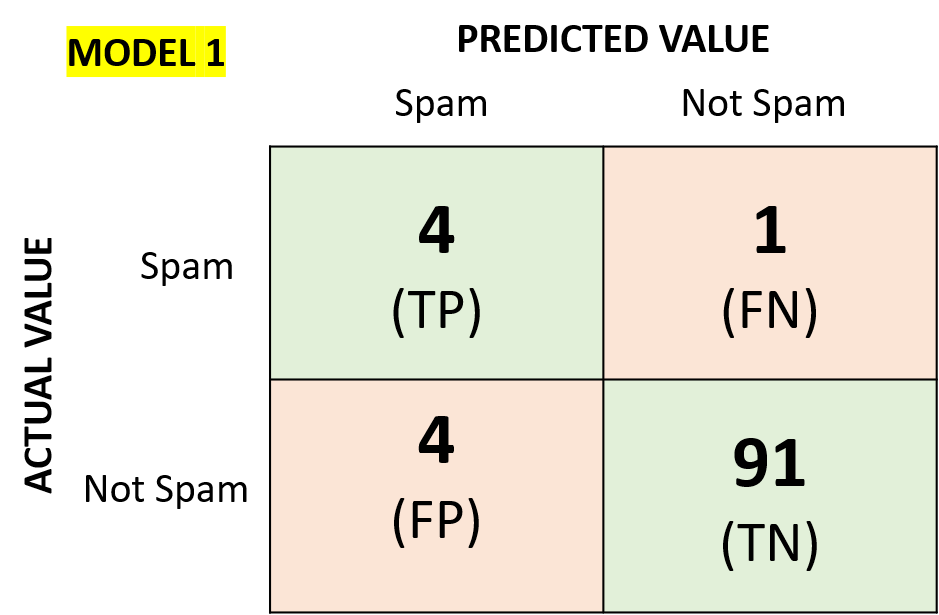
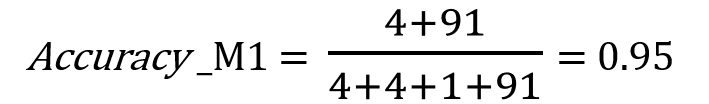
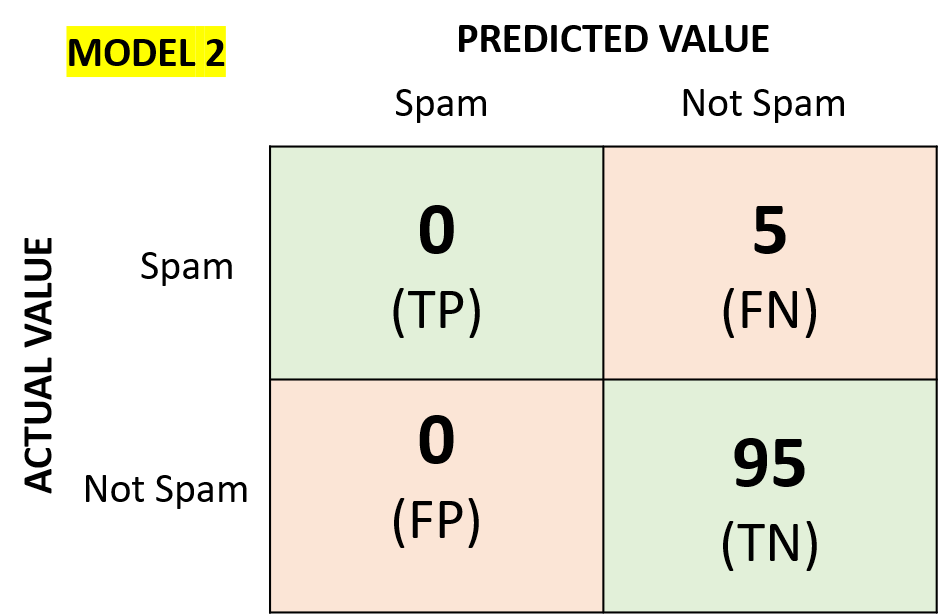
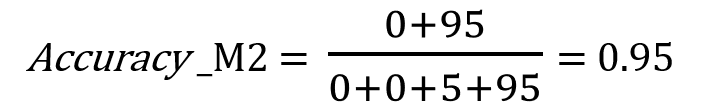
The accuracy of the two models “Accuracy_M1” and “Accuracy_M2” are the same as “0.95” even if the second model could not detect any spam email
(no “TP”), which is actually its main purpose.

The "Accuracy Pardox" is the paradoxical finding that accuracy is actually not a good metric for predictive models of classification problems.

So we need other metrics for evaluation of a classification model.
Let’s go back to our corona testkit model.

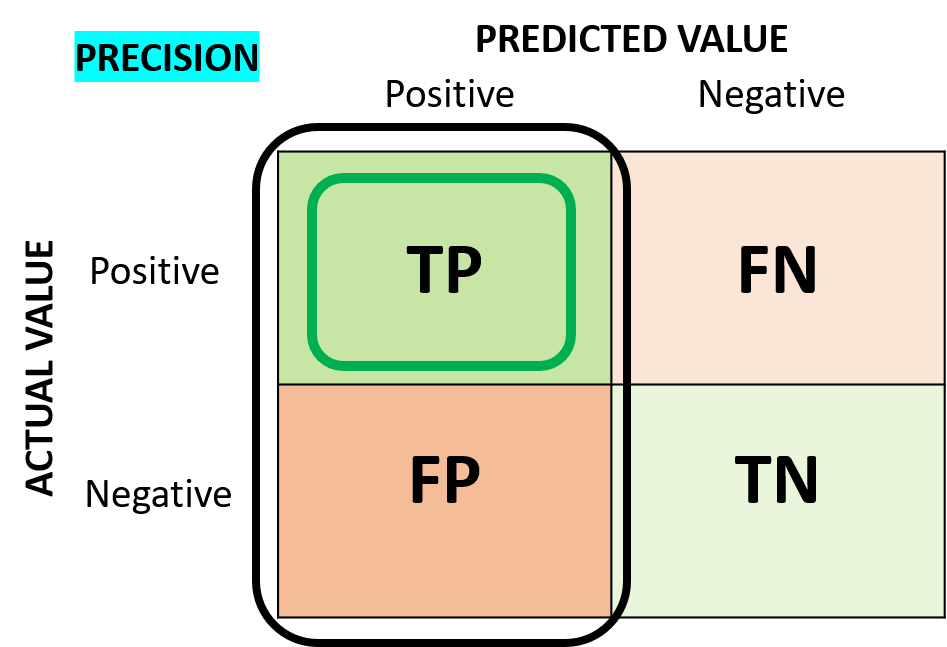
Precision

"Precision" is the ratio of correctly IDENTIFIED positive cases to all PREDICTED positive cases.
For Precision, we can focus on the vertical line of the follwing confusion matrix:

This is the formula how we calculate the precision:

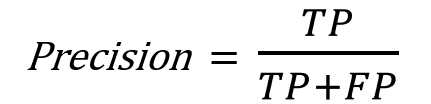
And this is the precision of our model:

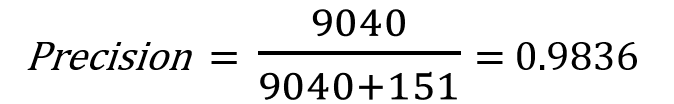
For our testkit model, Precision “1” means that the model gave the positive results only for people who actually have corona virus.

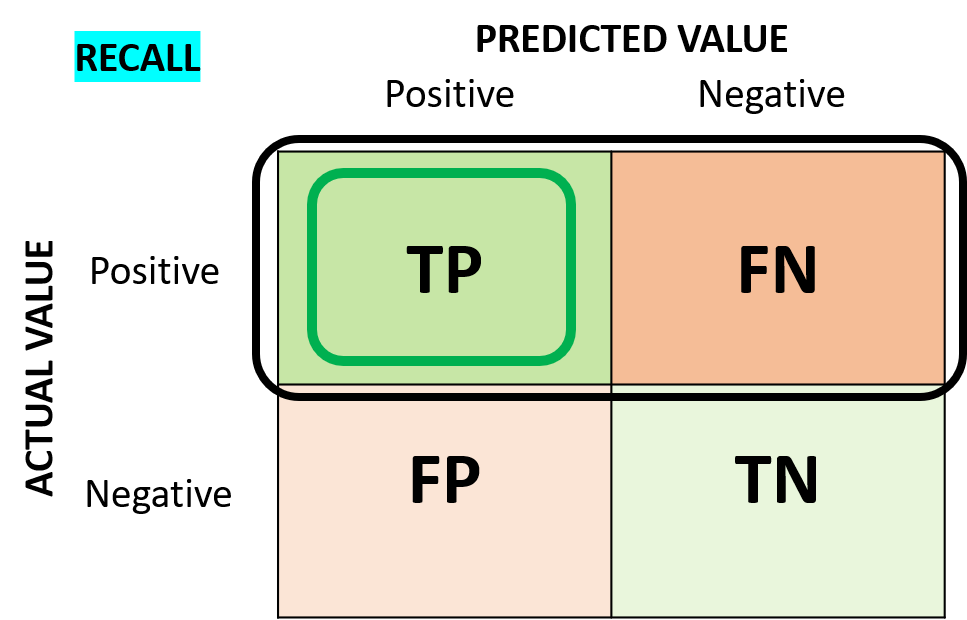
Recall

"Recall" is the ratio of correctly IDENTIFIED positive cases to all ACTUAL positive cases.
For Recall, we can focus on the horizontal line of the follwing confusion matrix:

This is the formula how we calculate the precision:

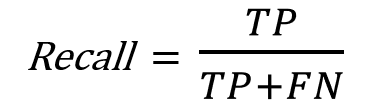
And this is the precision of our model:

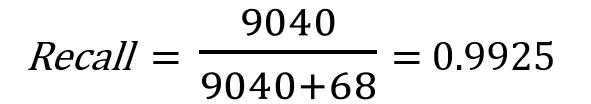
For our testkit model, Recall “1” means model does not wrongly predict people who does not have corona as positive.

F1-Score

Actually we want to know both of them:
1. if a model identifies all of our positive cases (from “Precision”)
2. if the model at the same time identifies only positive cases (from “Recall”)

"F1-Score" is the harmonic mean of "Precision" and "Recall" as we can see in the formula:

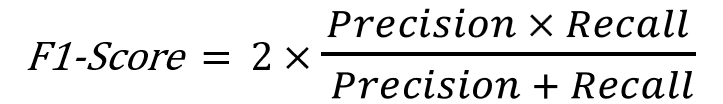
And this is the F1-Score of our model:

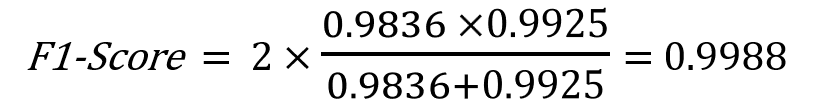
Since we know how to evaluate a model for binary classification, now we can evaluate a model for multiclass classification.

References

• Reference1: Evaluation of Model (in German)
• Reference2: Metrics for Evaluation (in German)

---